1 提出背景

为什么要引入RNN呢？

非常简单，之前我们的卷积神经网络CNN，全连接神经网络等都是单个神经元计算

但在序列模型中，前一个神经元往往对后面一个神经元有影响

比如

两句话

I like eating apples.

I want to have a apple watch

第一个苹果和第二个苹果的概念是不一样的，第一个苹果是红彤彤的苹果，第二个苹果是苹果公司的意思

如何知道

是因为apple的翻译参考了上下文，第一句话看到了eating这个单词，第二句话看到了watch这个单词

因而可见，对于语言这种时序信息，利用需要参考上下文进行

还有其他原因

拿人类的某句话来说，也就是人类的自然语言，是不是符合某个逻辑或规则的字词拼凑排列起来的，这就是符合序列特性。
语音，我们发出的声音，每一帧每一帧的衔接起来，才凑成了我们听到的话，这也具有序列特性、
股票，随着时间的推移，会产生具有顺序的一系列数字，这些数字也是具有序列特性。

2 RNN

具有时序功能，从某种意义来说，RNN也就具有了记忆功能，好比我们人类自己，为什么会受到过去影响，因为我们具有记忆能力。

同时只有记忆能力是不够的，处理后的信息得储存起来，形成“新的记忆”

对于RNN，可以分为单向RNN，和双向RNN，其中单向的是只利用前面的信息，而双向的RNN既可以利用前面的信息，也可以利用后面的信息。

2.1 RNN结构

RNN的基本单元包含以下关键组件：

输入 ($x_t$ )：表示在时间步 (t) 的输入序列。
隐藏状态 ($h_t$ )：在时间步 (t) 的隐藏状态，是网络在处理序列过程中保留的信息相当于ht里面藏着上下文信息
**每一步的输出(Oi)**：每一个时间步有一个输出Oi，Oi综合了当前时间步和之前的很多信息，那么对于某些特定任务，如分类什么的，就可以直接用Oi去做判断。很多时候直接把隐藏状态拿去做了输出

如下图，图片来自《动手学深度学习》

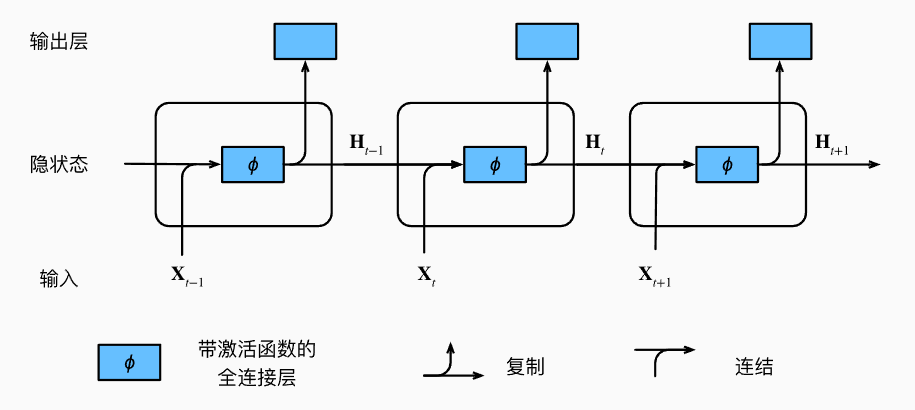
那么每一个隐状态是通过怎样的方式得到的呢？

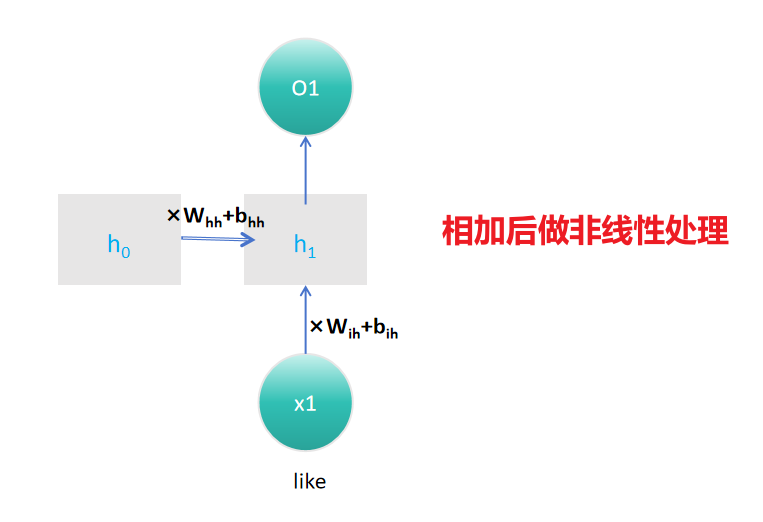
RNN的隐藏状态 (ht ) 的计算通过以下数学公式完成：

$h_t=tanh(W_{ih}x_t+b_{ih}+W_{hh}h_{t−1}+b_{hh}) $

这个公式展示了RNN如何根据当前输入 (xt ) 和前一个时间步的隐藏状态 (ht−1 ) 来计算当前时间步的隐藏状态 (ht )。其中 (tanh) 是双曲正切激活函数，用于引入非线性。

实际中我们可以看到

权重矩阵 ($W_{ih} , W_{hh} $)：分别是输入到隐藏状态和隐藏状态到隐藏状态的权重矩阵。
偏差 ($b_{ih} , b_{hh} $)： 对应的偏差。

第一个问题是每一个句子的长度不一致，你怎么用统一的矩阵呢？

只实现了一个单层神经元，可以通过获得句子长度知道时间步数t，进一步做相关的调整

2.2 RNN代码实现

代码实现首先实现上图的一个神经元

def rnn(inputs, state, params):
    # inputs的形状：(时间步数量，批量大小，词表大小)
    W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    # X的形状：(批量大小，词表大小)
    for X in inputs:
        H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h)
        Y = torch.mm(H, W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)

class RNNModelScratch: #@save
    """从零开始实现的循环神经网络模型"""
    def __init__(self, vocab_size, num_hiddens, device,
                 get_params, init_state, forward_fn):
        self.vocab_size, self.num_hiddens = vocab_size, num_hiddens
        self.params = get_params(vocab_size, num_hiddens, device)
        self.init_state, self.forward_fn = init_state, forward_fn

    def __call__(self, X, state):
        X = F.one_hot(X.T, self.vocab_size).type(torch.float32)
        return self.forward_fn(X, state, self.params)

    def begin_state(self, batch_size, device):
        return self.init_state(batch_size, self.num_hiddens, device)

然后利用循环，根据语句长度做预测判断，损失函数计算优化

def predict_ch8(prefix, num_preds, net, vocab, device):  #@save
    """在prefix后面生成新字符"""
    state = net.begin_state(batch_size=1, device=device)
    outputs = [vocab[prefix[0]]]
    get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))
    for y in prefix[1:]:  # 预热期
        _, state = net(get_input(), state)
        outputs.append(vocab[y])
    for _ in range(num_preds):  # 预测num_preds步
        y, state = net(get_input(), state)
        outputs.append(int(y.argmax(dim=1).reshape(1)))
    return ''.join([vocab.idx_to_token[i] for i in outputs])

2.3 代码简洁实现

往往通过一个nn.RNN来实现

nn.RNN(input_size, hidden_size, num_layers=1, nonlinearity=tanh, bias=True, batch_first=False, dropout=0, bidirectional=False)

参数说明

input_size输入特征的维度，一般rnn中输入的是词向量，那么 input_size 就等于一个词向量的维度
hidden_size隐藏层神经元个数，或者也叫输出的维度（因为rnn输出为各个时间步上的隐藏状态）
num_layers网络的层数，一般可以默认为1
nonlinearity激活函数
bias是否使用偏置
batch_first输入数据的形式，默认是 False，就是这样形式，(seq(num_step), batch, input_dim)，也就是将序列长度放在第一位，batch 放在第二位
dropout是否应用dropout, 默认不使用，如若使用将其设置成一个0-1的数字即可
birdirectional是否使用双向的 rnn，默认是 False
注意某些参数的默认值在标题中已注明

1	rnn_layer = nn.RNN(input_size=vocab_size, hidden_size=num_hiddens, )

定义模型，其中vocab_size = 1027, hidden_size = 256

Qodicat's World

Try something new and interesting

1 提出背景

2 RNN

2.1 RNN结构

2.2 RNN代码实现

2.3 代码简洁实现

谢谢你给我买一个棒棒糖